La trilatération permet de dessiner le plan d’un espace avec des outils aussi simples qu’un décamètre, une règle et un compas. Pour illustrer la méthode, nous allons représenter à l’échelle 1/100° l’implantation des arbres repérés sur la photographie ci-dessus par O1, O2 et O3, et du poteau A. Le plan obtenu tiendra sur une page A4.

Avant de tracer le plan, il faut relever les mesures. Pour cela, vous devez utiliser un décamètre, une feuille de papier et un crayon.

  • Mesurez avec le décamètre, les distances en mêtres entre O1 et O2, O1 et O3, O1 et A, O2 et O3, O2 et A, et O3 et A.
  • Arrondissez les au premier chiffre après la virgule le plus proche.
  • Inscrivez les dans un tableau, comme ci-dessous.

Vous obtenez alors un tableau qui ressemble à celui ci-dessous.

mO1O2O3
O105,69,8
O25,606,5
O39,86,50
A8,06,12,5

Une fois le tableau renseigné, prenez une autre feuille A4, un double-décimètre, un crayon et un compas. Vous voilà prêt à traduire le tableau en plan. La conversion à l'échelle 1/100° est instantanée : les nombres du tableau sont les mesures en centimètres à appliquer sur le plan. La figure ci-dessous montre le tracé à réaliser.

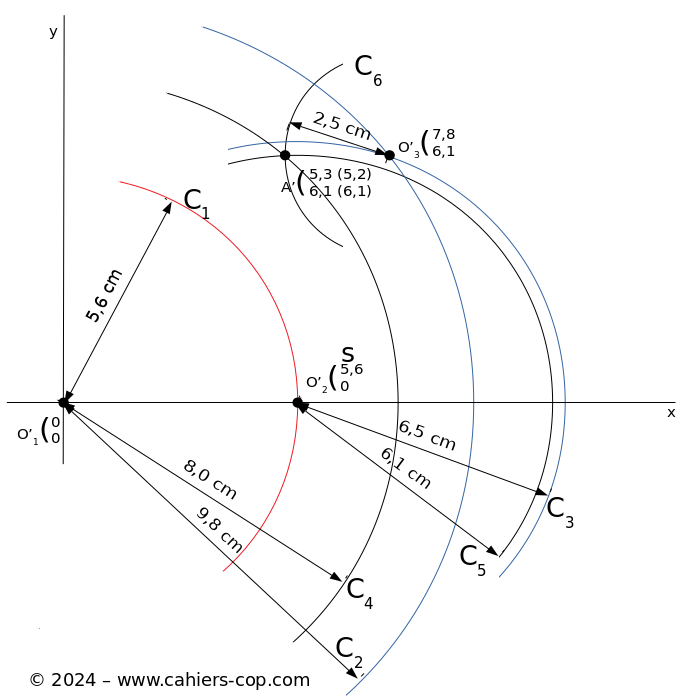
  1. Représentez le point O1 en bas à gauche de la feuille et appelez O'1 sa représentation.
  2. Tracez un axe dans la largeur de la feuille passant par O'1.
  3. Tracez le cercle C1, dont le rayon est la distance entre 01 et 02 divisée par 100 (ce qui revient à garder la valeur de la mesure et à changer l’unité en cm).
  4. Nommez O'2 l’intersection entre l’arc de cercle C1 et l’axe x.
  5. Mesurez la distance entre O1 et O3, et tracez C2.
  6. Reproduisez l’opération avec O2 et O3, et tracez C3.
  7. C2 et C3 se coupent en deux points symétriques par rapport à l’axe x. Nommez O'3 l’intersection qui se trouve en haut de la feuille. Vous venez de tracer votre repère sur le plan.
  8. Pour représenter l’emplacement du poteau A sur le plan, il suffit de mesurer dans l’orde ses distances à O1, O2 et O3, de les diviser par 100, et de tracer avec les écarts obtenus, les cercles C4, C5 et C6. L’intersection des trois cercles correspond à l’implantation du poteau.

Une autre application de la trilatération et la navigation à l’aide d’une carte, d’une règle, d’un compas et d’un instrument de télémétrie. Illustrons ce concept en nous promenant dans l’espace arboré ci-dessus.

Après avoir repéré les trois arbres et leur représentation sur le plan, il suffit de mesurer, par exemple avec un télémètre laser, la distance vous séparant de chacun des arbres et de tracer les cercles avec les rayons correspondant à la distance divisée par 100. L’intersection des trois cercles sera votre position.

Comme nous le voyons, la trilatération est une méthode simple de topographie ou de navigation, dès l’instant où les outils classiques de la géométrie sont utilisés. Mais qu’en est-il pour un robot qui, a priori, n’utilise pas une règle et un compas ? La géométrie analytique est alors la solution.

En appellant :

  • (x1;y1), (x2;y2) et (x3;y3) les coordonnées respectives des points O1, O2 et 03 dans un repère cartésien ;
  • et d1, d2 et d3 les distances respectives à O1, O2 et 03 du point M de coordonnées (x;y)
On a : x = − y 1 F 2,3 + y 2 F 3,1 + y 3 F 1,2 K y = x 1 F 2,3 + x 2 F 3,1 + x 3 F 1,2 K avec : F i , j = y ² i + x ² i − y ² j − y ² i + d ² j − d ² i K = 2 ( y 1 ( x 3 − x 2 ) + y 2 ( x 1 − x 3 ) + y 3 ( x 2 − x 1 ) ) alignl { "On a :" } newline alignl {x=-{{ y_1 F_2,3 + y_2 F_3,1 + y_3 F_1,2} over {alignc K}}} newline alignl {y={ x_1 F_2,3 + x_2 F_3,1 + x_3 F_1,2} over {alignc K}} newline alignl { "avec :" } newline alignl {F_i,j=y²_i + x²_i - y²_j -y²_i + d²_j - d²_i} newline alignl { K=2(y_1(x_3 - x_2)+y_2(x_1-x_3)+y_3(x_2-x_1))} newline

Donc, si le robot reçoit dans l’ordre les valeurs de x1, y1, d1, x2, y2, d2, x3, y3 et d3, alors, il peut calculer sa position à l’aide d'un programme comme celui ci-dessous. Celui-ci est écrit en C, car c’est le langage de l’Arduino, plate-forme utilisée dans le projet du Couloir de nage pour satellite.

// position

// Calcule la position d'un point par trilatération

// Version : 1.0

// Date : 02/02/2024

// Utilisation

// >position x1 y1 d1 x2 y2 d2 x3 y3 d3

//O1 : (x1;y1) d1

//O2 : (x2;y2) d2

//O3 : (x3;y3) d3

//K=

//F(1,2)=

//F(2,3)=

//F(3,1)=

//X Y

#include 

float x[3],y[3],d[3];

float carre(float a) {

return (a*a);

}

float F(int i,int j) {

return (carre(y[i])+carre(x[i])-carre(y[j])-carre(x[j])+carre(d[j])-carre(d[i]));
 
}



void main (int argv, char *argc[]) {

int i;

float K,X,Y;

if(argv==10) {

    for(i=0;i<3;i++) {

        sscanf(argc[3*i+1],"%f",&x[i]);

        sscanf(argc[3*i+2],"%f",&y[i]);

        sscanf(argc[3*i+3],"%f",&d[i]);

        printf("O%d : (%f;%f) %f\n",i+1,x[i],y[i],d[i]);

        }

    K=2*(y[0]*(x[2]-x[1])+y[1]*(x[0]-x[2])+y[2]*(x[1]-x[0]));

    printf("K=%f\n",K);

    printf("F(1,2)=%f\n",F(0,1));

    printf("F(2,3)=%f\n",F(1,2));

    printf("F(3,1)=%f\n",F(2,0));

    X= -(y[0]*F(1,2)+y[1]*F(2,0)+y[2]*F(0,1))/K;

    Y= (x[0]*F(1,2)+x[1]*F(2,0)+x[2]*F(0,1))/K;

    printf("%f %f\n",X,Y);

    } else {

    printf("%s x1 y1 d1 x2 y2 d2 x3 y3 d3\n", argc[0]);

    }

}

Exemple :

>./position 0 0 8 5.6 0 6.1 7.8 6.1 2.5

O1 : (0.000000;0.000000) 8.000000

O2 : (5.600000;0.000000) 6.100000

O3 : (7.800000;6.100000) 2.500000

K=68.320000

F(1,2)=-58.150002

F(2,3)=-97.650002

F(3,1)=155.800003

5.191964 6.131586

Si on compare pour A' les coordonnées obtenues avec le logiciel (nombres entre parenthèses) avec celles obtenues graphiquement, on observe une erreur de 1 mm, soit de l'ordre de grandeur de la précision du double-décimètre.

La question qui se pose maintenant est comment déterminer les valeurs de x1, y1, d1, x2, y2, d2, x3, y3 et d3 pour un robot ? La réponse sera abordée dans un prochain billet.